Controlling for large language models in decision making chains

I think it's both useful and important to distinguish the information processes and outputs which have had artificial knowledge agent input. The usefulness of these probabilistic knowledge fetchers is based on how well they can help a human knowledge agent solve a problem, often brought to them by another human. To solve the problem the first human will probably involve at least one other.

We often end up needing to solve a joint optimisation problem in order to get the problem solved. The ideal use case for me is using AI as the probabilistic prime mover and critique that with the causal understanding of humans. How often the large language model throws a fair dice is a valid question and this is one reason to always test two large language models on the same question at the same time.

I'm interested in instrument effects because they're observable once we put the two side by side and compare how they have presented the output of their information process. We can see how the weft of the informational output follows the warp of the instrument, which are observable in artificial knowledge agent information mediations. For example, I had to ask 14 questions to get Gemini to tell me who the 47th President of the US was. Instrument effects can be found or made visible.

I think instrument effects produce non-negligible predictable impacts on the information outcome, another reason to have at least two probabilistic word calculators on a decision problem. I also need another human knowledge agent, an interested expert who knows how to use a large language model. They needed to be interested and be more likely to have a positive outlook. They needed to know how to coax as much of the truth out of the large language model as it cares to give up.

In this pair we could generate a useful scientific dialectic, where I could give an expert question to them to then ask an expert question of the large language model. We both had rigour in our domain and had the rare advantage of having met many years ago, who held different views and were adaptable enough to build a dialogue. We both were both mediating the knowledge of agents; they were engaging with the large language model, and I was engaging with a third-party subject matter expert with a challenging problem.

I was able to cover the risk of not knowing what good looked like and they got an interesting problem to work on. They knew the subject matter but not the third-party expert and I wrote the original prompt which bridged the two. I didn't have an interest in the desired outcome of the third party and could just focus on the process of presenting a clear problem, given my assessment of their case.

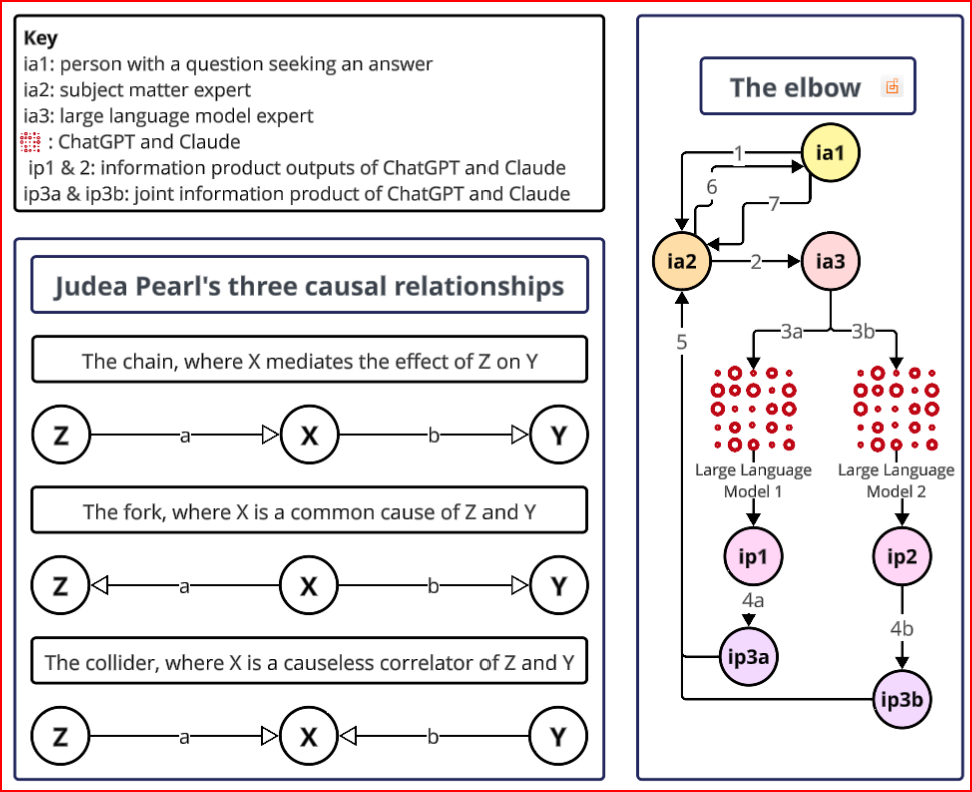
The third party, my expert colleague and I form a decision making 'elbow'; I'm the elbow, the third party is the wrist, and my expert colleague is the shoulder. If we were able to optimise our decision work, then we could lift quite a lot of weight. I remained uninvolved in the performance of the large language model beyond the initial prompt and my colleague remained uninvolved in the relationship with the third party. It is a strong position to generate evidence from.

I then prepared for the answer, which may or may not be close to the truth. Here the physics concept of the oracle can be leveraged. An oracle is something that we use to test conjectures and won't be a thing until quantum computation develops. The oracle will remind me there was a non-zero % chance that the one-time information event generated by one of the two large language models might yield exactly the right answer to the question.

There seemed a much higher % chance that the information event would be mostly right and there was an uncomfortably high % chance the artificial information agent makes something up, leaves something out, is flat out wrong or in some way deceives my colleague. While we can roll the dice a million times in a thought experiment, most events tend to happen just once, and the result is what will forever be. Many possibilities collapse rapidly into one. Fortunately, the math around sampling a possibility horizon helps here.

Because the artificial knowledge agent is using probabilistic methods to construct its information product, the overall information process is improved as if the human knowledge agent had been using similar methods. This means we can look at one information product from an artificial knowledge agent and see it as representative of what that agent would otherwise produce across 100 tests. We can just ask the question once and accept the answer as fairly accurate. We just need that one expert question to be expertly asked.

To that end I've been working with a colleague to take the role of the LLM wrangler and using the elbow to work through third-party's structural problem, where two good rules create a wrong and was something I needed to understand better. We've been stipulating that the response use counterfactual language, firstly as a joint language but also as a test stage for hallucinations and other instrument effects. They're as good at thinking causally as we are thinking probabilistically. Once we account for both, we can reliably get reliable answers, within a reliable range.

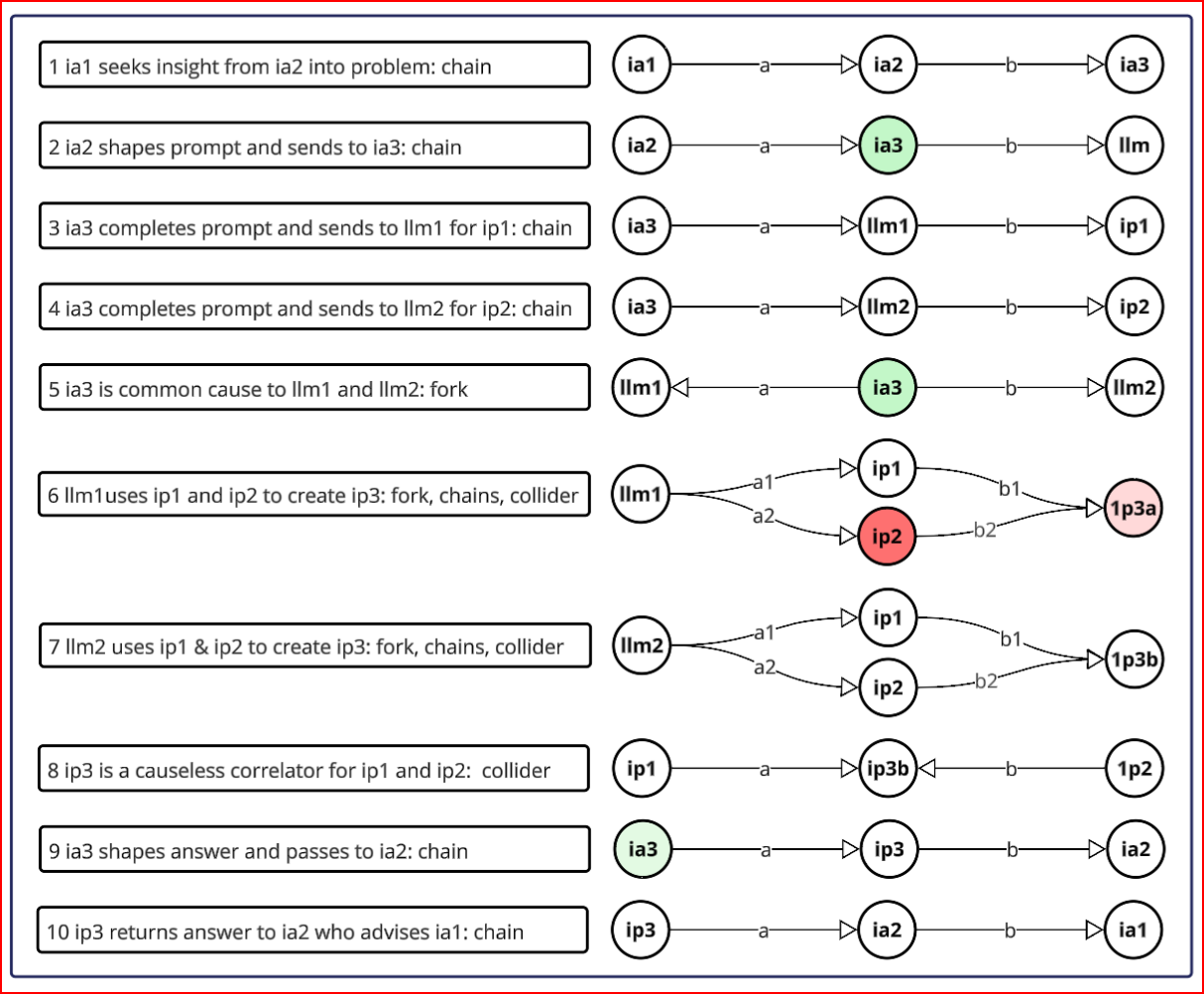
The elbow is shown beside the three causal relationships Judea Pearl proposed to use to describe the underlying power dynamic in a system. There only being three possible types is a clue to there often being a lot of relationships and interactions to examine. We can disarticulate the elbow to identify the causal map in play and surface 10 causal relationships, one of which produced a lesser information product. We can also see the mediating influence of the LLM wrangler.

LLM1 couldn't synthesize the output of LLM2, which could synthesize for LLM1. I took that as the decider and adopted the synthesis of LLM2. Because I had the domain knowledge and problem statement, I could choose between LLM1 and LLM2, avoiding the problem of the unreliable AI advisor and obtain the benefit of an expert sample of expert material.

I think one of Schrödinger's main lessons is for someone to not look in the box. Leaving some things unobserved is paradoxically useful, similar to adding randomness to a problem. It's good to control for experiments like these because the identity of the observer will have a non-negligible effect on the observation, we can reduce the number of hidden correlations, and we can work within a relatively simple problem space. This technique is working for us at the moment, and I'll update this post as we go.